
Sources of error in polls
The calender has turned to September and we’re now getting into the election season proper, which seems like as good a good time as any to talk about polls.
Specifically, all of things that go into a poll, and all of the ways in which these different components of a poll are susceptible to error, some of the errors controllable and others not, some of them caused by the pollster, others by random variation.
One thing we need to get out of the way right off the bat when talking about polls, political polls specifically, is that they are susceptible to error being introduced at almost every stage of the process and the amount of effort expended to mitigate those sources of error are almost always directly tied to the amount of money and time spent on the poll.
Said another way, better polling costs more money and time, the two things that are most important to every political campaign and that they invariably have a finite supply of.
But even if you had an unlimited amount of money and time to construct the perfect poll and administer it in the most effective way possible, there will still be some amount of random error, or more accurately, the possibility of random error.
It’s no surprise than that any single poll can be wildly off the mark. What I’m going to discuss here are all the different steps along the way that can contribute to that potential error, some of which are within the pollsters control and some of which are not.
Definitionally these two types of error are called biased and random. A biased error is an error that the pollsters themselves introduces into the data, while random error is simply the amount of variation you can expect with a random distribution of data.
To identify all the possible sources of error in polls we need to start at the beginning.
The process of polling breaks down into two basic premises; one, that a sample of a population can approximate the characteristics of that population and two, that the answers respondents give to questions accurately reflect their true feelings.
For each of these premises to be true, great care needs to be taken in designing a survey. If the sample doesn’t accurately reflect the population or if the questions asked are confusing or leading, the results of the survey will suffer.
The Sample
The sample is the group of people to be polled, the potential respondents. Ideally you want the sample to reflect the target population as closely as possible.
The potential variation between the distribution of the sample and the distribution of the target population is known as the margin of error. The graph below does a good job of illustrating this point: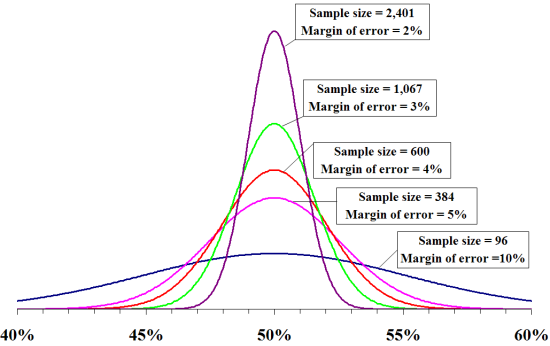
What you can see is as the number of people sampled increases, the amount of variance narrows. This is because of the law of large numbers:
In probability theory, the law of large numbers (LLN) is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value, and will tend to become closer as more trials are performed.
When a polls margin of error is discussed, the error it refers to is the possible range of variation between the people sampled and the actual target population, usually with a confidence interval of 95%.
Said differently, a margin of error of 4.5% means that 95% of the time the sample population distribution will be within 4.5% of the target population distribution on the high or low side. Meaning that 5% of the time the sample distribution will not be within 4.5% of the target population distribution.
The Sample Frame
Before we can gather a sample though, we need to define who has a chance to actually be sampled. This is the sample frame, the parameters of who will have a chance of being included in the sample.
In most election polls the sample frame is registered voters, from which a likely voter screen will often be applied. There is sometimes also a geographic frame; the State of Minnesota, Senate district 42, and Minneapolis are all examples of geographic frames. If you were polling the Minneapolis Mayoral race, you would only want to sample people who live in Minneapolis.
The sample frame is the first way in which error can effect a poll, in this case bias error.
In Minnesota for instance we have same day voter registration, meaning that anyone can be a voter. That said, only a certain percentage of voters in any given election are same day registrants, in fact the vast majority of voters will already be registered.
Regardless, this population of unregistered voters should still be accounted for in the sample frame as opposed to just limiting your sample to already registered voters.
Some pollsters have historically approached this differently in Minnesota, the HHH/MPR poll uses a random digit dialing method thereby everyone with a phone has an equal chance of being a respondent. SurveyUSA, on the other hand, doesn’t even attempt to account for this and only talks to registered voters in their polls.
While it seems like an error on the part of SurveyUSA to ignore these non-registered but otherwise eligible voters, their results in Minnesota over the years have been much more accurate than that of the HHH/MPR poll, which does include these voters in their sample frame.
Ideally a pollsters sample frame should encompass everyone who can vote in the election being polled but this isn’t always the case, for various reasons. In the case of the examples I cites, I suspect each organization has their own reasons for doing things the way they do.
The Sample
Once you have your sample frame, you can than collect your sample. And, of course, there can be error associated with the gathering of the sample beyond the random sampling error discussed earlier.
While SurveyUSA had a good cycle in 2010 it was not perfect, in fact they had a pretty bad run in one district in particular, VA-5, Tom Perriello’s former district. During that summer they released a couple of polls showing Perriello down by 20+ points which contradicted all the other polling that had been done on the race showing a much closer contest.
To their credit SurveyUSA was also skeptical of their numbers and eventually made a change to their methodology for that district. The problem, they discovered, was a flawed voter list from which they were drawing their sample. For the rest of the campaign they instead used a random-digit dialing method to conduct their surveys of VA-5 and their results after that were significantly more accurate.
So why then don’t they use random-digit dialing as a standard practice?
For the simple reason that random-digit dialing isn’t as accurate or efficient as a good list.
Random-digit dialing’s accuracy or lack thereof, is directly tied to it’s randomness. A purely random sample will usually get you close to the actual population distribution, but sometimes it won’t and randomness itself isn’t the goal here, a sample that accurately reflects the population being polled is.
The example of flipping a coin works to illustrate this point. When flipping a coin there is a 50/50 chance that it will land on either heads or tails. If you flip a coin 10 times you will usually end up with five heads and five tails.
But you will sometimes end up with a 6/4 split. Sometimes a 7/3 split. Sometimes even an 8/2 split and so on. The point is that flipping a coin is random but randomness can sometimes lead to distributions that are not proportionate of the population at large. Which in the case of the coin, is 50/50, one head, one tail.
There are two ways to try and mitigate sampling error, the first and more expensive, is to simply increase the number of respondents you hope to convert. But what is usually done, because it is more cost effective, is to employ a stratified sampled:
In statistical surveys, when subpopulations within an overall population vary, it is advantageous to sample each subpopulation (stratum) independently. Stratification is the process of dividing members of the population into homogeneous subgroups before sampling.
As an example of how a stratified sample could be employed we can look at the HHH/MPR poll that came under criticism following the 2010 Governor’s race in which their final poll showed a 12 point Dayton lead while the final results were quite a bit closer than that.
Both an internal and external audit were done of that poll and one of the conclusions was that geographic weighting of the sample was something that should be employed in future polls as a way of correcting the higher response rates they achieved in with 612 numbers compared with other area codes.
While most of what’s in the audit applies to the actual data collection part of the process, this is an example of where a stratified sample could have helped. If they knew ahead of time that they wanted x% of respondents to come from the 612 area code, they could have stratified the sample by area code so that they would protect themselves from a higher response rate in any one area code.
And since sub-population weighting simply introduces the possibility for yet more error, by magnifying any error present, it would seem prudent to address this issue before the data collection process even begins as opposed to having to do after the fact corrections to already gathered data.
The data you collect can only be as good as the sample from which it’s collected, so as many problems as you can address with the sample itself, the better the data that you collect will be and the less manipulation of that data you will have to do to bring the demographics of it in line with the actual population.
That’s the theory at least.
The Data Collection Process
Once we have our sample, we can begin phase two of the polling process, the data collection phase, or the actual calling of people and asking them questions.
Like phase one, the sample phase, phase two can be effected by both random and bias error. But discussion of this part of the polling process and the error that can effect it, will have to wait for part 2, because I’m already over 1,700 (!) words with this post.
Thanks for your feedback. If we like what you have to say, it may appear in a future post of reader reactions.


